ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Представление о плоскости в пространстве позволяет получить, к примеру, поверхность стола или стены. Однако, стол или стена имеют конечные размеры, а плоскость простирается за их границы в бесконечность.

Рассмотрим две пересекающиеся плоскости. При пересечении они образуют четыре двугранных угла с общим ребром.

Вспомним, что из себя представляет двугранный угол.

В реальности мы встречаемся с предметами, которые имеют форму двугранного угла: например, приоткрытая дверь или полураскрытая папка.

При пересечении двух плоскостей альфа и бета получим четыре двугранных угла. Пусть один из двугранных углов равен (фи), тогда второй равен (1800 -), третий, четвертый (1800-).

Рассмотрим случай, когда один из двугранных углов равен 900.

Тогда, все двугранные углы в этом случае равны по 900.

Введем определение перпендикулярных плоскостей:

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.

Угол между плоскостями сигма и эпсилон равен 90 градусов, значит плоскости перпендикулярны

Приведем примеры перпендикулярных плоскостей.

Стена и потолок.

Боковая стенка и крышка стола.

Сформулируем признак перпендикулярности двух плоскостей:

ТЕОРЕМА: Если одна их двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Докажем этот признак.

По условию известно что прямая АМ лежит в плоскости α, прямая АМ перпендикулярна плоскости β,

Доказать: плоскости α и β перпендикулярны.

Доказательство:

1) Плоскости α и β пересекаются по прямой АР, при этом АМ АР, так как АМ β по условию, то есть АМ перпендикулярна к любой прямой, лежащей в плоскости β.

2) Проведем в плоскости β прямую AТ перпендикулярную AР.

Получим угол ТAМ - линейный угол двугранного угла. Но угол ТAМ = 90°, так как МА β. Значит, α β.

Что и требовалось доказать.

Из признака перпендикулярности двух плоскостей имеем важное следствие:

СЛЕДСТВИЕ: Плоскость, перпендикулярная к прямой, по которой пересекаются две плоскости, перпендикулярна к каждой из этих плоскостей.

То есть: если α∩β=с и γ с, то γ α и γ β.

Докажем это следствие: если плоскость гамма перпендикулрна к прямой с то по признаку параллельностидвух плоскостей гамма перпендикулярна к альфа. Аналогично и гамма перпендикулярна бета

Указанное следствие переформулируем для двугранного угла:

Плоскость, проходящая через линейный угол двугранного угла перпендикулярна ребру и граням этого двугранного угла. Другими словами, если мы построили линейный угол двугранного угла, то проходящая через него плоскость перпендикулярна ребру и граням этого двугранного угла.

Дано: ΔАВС, С = 90°, АС лежит в плоскости α, угол между плоскостями α и ABC = 60°, АС = 5 см, АВ = 13 см.

Найти: расстояние от точки В до плоскости α.

1) Построим ВК α. Тогда КС - проекция ВС на эту плоскость.

2) ВС АС (по условию), значит, по теореме о трех перпендикулярах (ТТП), КС АС. Следовательно, ВСК - линейный угол двугранного угла между плоскостью α и плоскостью треугольника АВС. То есть ВСК = 60°.

3) Из ΔВСА по теореме Пифагора:

Ответ ВК равно 6 корней из трех см

Практическое использование (прикладной характер) перпендикулярности двух плоскостей.

Перпендикулярность плоскостей Определение. Две плоскости называются перпендикулярными, если линейный угол при ребре двугранного угла между этими плоскостями - прямой.
Признак перпендикулярности плоскостей. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Доказательство. Пусть a и ? - две пересекающиеся плоскости, с - прямая их пересечения и а - прямая перпендикулярная плоскости ? и лежащая в плоскости a . А - точка пересечения прямых a и с. В плоскости ? из точки А восстановим перпендикуляр, и пусть это будет прямая b . Прямая а перпендикулярна плоскости ? , а значит она перпендикулярна и любой прямой в этой плоскости, то есть прямые b и с перпендикулярны. Угол между прямыми а и Ь - линейный плоскостями a и ? и равен он 90°, так как прямая а перпендикулярна прямой b (подоказанному).Поопределениюплоскости a и ? перпендикулярны.

Теорема 1 . Еслииз точки,принадлежащейодной из двух перпендикулярных плоскостей,провести перпендикуляр к другой плоскости, то это перпендикуляр полностью лежит в первой плоскости.
Доказательство. Пусть a и ? - перпендикулярные плоскости и с - прямая их пересечения, А - точка лежащаявплоскостиa и не принадлежащая прямой с. Пустьперпендикуляр к плоскости ? проведенный из точки А , не лежит в плоскости a , тогда точка С – основание этого перпендикуляра лежит в плоскости ? и не принадлежит прямой с. Из точки А опустим перпендикуляр АВ напрямую с. Прямая АВ перпендикулярна плоскости (использую теорему 2). Через прямую АВ и точку С проведем плоскость ? (прямая и точка определяют плоскость, причем только одну). Мы видим, что в плоскости ? из одной точки А на прямуюВС проведено два перпендикуляра, чего быть не может, значит прямая АС совпадает с прямой АВ, а прямая АВ в свою очередь полностью лежит в плоскости a .

Теорема 2 . Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
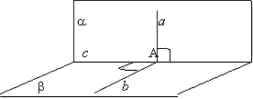Доказательство. Пусть a и ? - две перпендикулярные плоскости, с - прямая их пересечения и а - прямая перпендикулярная прямой с и лежащая в плоскости a . А - точка пересечения прямых а и с. В плоскости ? из точки А восстановим перпендикуляр, и пусть это будет прямая b . Угол между прямыми а и b - линейный угол при ребре двугранного угла между плоскостями a и ? и равен он 90°, так как плоскости a и ? перпендикулярны. Прямая а перпендикулярна прямой b (по доказанному) и прямой с по условию. Значит прямая а перпендикулярна плоскости? (

Ðассматривается отношение перпендикулярности плоскостей - одно из важнейших и наиболее используемых в геометрии пространства и ее приложениях.

Из всего разнообразия взаимного расположения

двух плоскостей особого внимания и изучения заслуживает то, при котором плоскости перпендикулярны друг другу (например, плоскости смежных стен комнаты,

забора и участка земли, двери и пола и т. п. (рис. 417, а–в).

Приведенные примеры позволяют увидеть одно из основных свойств отношения, которое мы будем изучать, - симметричность расположения каждой из плоскостей относительно другой. Симметрия обеспечивается тем, что плоскости вроде бы «сотканы» из перпендикуляров. Попробуем уточнить эти наблюдения.

Пусть имеем плоскость α и прямую с на ней (рис. 418, а). Проведем через каждую точку прямойс прямые, перпендикулярные плоскости α. Все эти прямые параллельны между собой (почему?) и составляют, на основании задачи 1 § 8, некоторую плоскость β (рис. 418, б). Естественно назвать плоскость βперпендикуляр­ ной плоскости α.

В свою очередь, все прямые, лежащие в плоскости α и перпен- дикулярные прямойс , образуют плоскость α и перпендикулярны плоскости β (рис. 418, в). Действительно, еслиа - произвольная такая прямая, то она пересекает прямуюс в некоторой точкеМ . Через точкуМ проходит в плоскости β перпендикулярная α пря- маяb , поэтомуb а . Следовательно,а с, а b , поэтомуа β. Таким образом, плоскость α перпендикулярна плоскости β, а пря- маяс является линией их пересечения.

Две плоскости называются перпендикулярными, если каждая из них образована прямыми, перпенди­ кулярными второй плоскости и проходящими через точки пересечения этих плоскостей.

Перпендикулярностьплоскостейαиβобоз- начается привычным уже знаком: α β.

Одну из иллюстраций этого определения можно представить, если рассмотреть фраг- мент комнаты дачного домика (рис. 419). В нем пол и стена сложены из досок, перпен- дикулярных соотвественно стене и полу. По- этому они перпендикулярны. На практике

это означает, что пол горизонтален, а стена вертикальна.

Приведенное определение трудно использовать при фактичес- кой проверке перпендикулярности плоскостей. Но если внима- тельно проанализировать рассуждения, которые привели к этому определению, то видим, что перпендикулярность плоскостей α и β обеспечило наличие в плоскости β прямойb , перпендикулярной плоскости α (рис. 418, в). Мы пришли к признаку перпендику- лярности двух плоскостей, который чаще всего применяется на практике.

406 Перпендикулярность прямых и плоскостей

Теорема 1 (признак перпендикулярности плоскостей).

Если одна из двух плоскостей проходит через прямую, перпендикулярную второй плоскости, то эти плоскости перпендикулярны.

 Пусть плоскость β проходит через прямуюb , перпендику- лярную плоскости α ис - линия пересечения плоскостей α и β (рис. 420, а). Все прямые плоскости β, параллельные прямойb и пересекающие прямуюс , вместе с прямойb образуют плоскость β. По теореме о двух параллельных прямых, одна из которых пер- пендикулярна плоскости (теорема 1 § 19), все они вместе с прямойb перпендикулярны плоскости α. То есть плоскость β состоит из прямых, проходящих через линию пересечения плоскостей α и β и перпендикулярных плоскости α (рис. 420, б).

Теперь в плоскости α через точку А пересечения прямыхb ис проведем прямуюа , перпендикулярную прямойс (рис. 420, в). Прямаяа перпендикулярна плоскости β, по признаку перпен- дикулярности прямой и плоскости (а с , по построению,а b , так какb α). Повторив предыдущие рассуждения, получим, что плоскость α состоит из прямых, перпендикулярных плоскости β, проходящих через линию пересечения плоскостей. Согласно оп- ределению, плоскости α и β перпендикулярны.■

Приведенный признак дает возможность устанавливать пер- пендикулярность плоскостей или же обеспечивать ее.

П р и м е р 1 . Прикрепить щит к столбу так, чтобы он был распо- ложен вертикально.

 Если столб стоит вертикально, то достаточно приложить произвольно щит к столбу и закрепить его (рис. 421, а). Согласно рассмотренному выше признаку, плоскость щита будет перпенди- кулярна поверхности земли. В этом случае задача имеет беско- нечное множество решений.

Если же столб стоит наклонно к земле, то достаточно к столбу прикрепить вертикальную рейку (рис. 421, б), а затем щит при- крепить и к рейке, и к столбу. В этом случае положение щита бу- дет вполне определённым, поскольку столб и рейка определяют единственную плоскость.■

В предыдущем примере «техническое» задание свелось к мате- матической задаче о проведении через данную прямую плоскос- ти, перпендикулярной другой плоскости.

П р и м е р 2 . Из вершиныA квадратаABCD проведен перпен- дикулярный его плоскости отрезокAK, AB = AK = а.

1) Определить взаимное расположение плоскостей AKC иABD ,

AKD и ABK.

2) Построить плоскость, проходящую через прямую BD перпенди- кулярно плоскостиABC.

3) Провести через середину F отрезкаKC плоскость, перпендику- лярную плоскостиKAC .

4) Найти площадь треугольника BDF.

 Построим рисунок, соответствующий условию примера (рис. 422).

1) Плоскости AKC иABD перпендикуляр- ны, по признаку перпендикулярности плос- костей (теорема 1):AK ABD , по условию. ПлоскостиAKD иABK также перпендику-

лярны, по признаку перпендикулярности плоскостей (теорема 1). Действительно, прямаяAB , через кото- рую проходит плоскостьABK , перпендикулярна плоскостиAKD , по признаку перпендикулярности прямой и плоскости (теорема 1 § 18):AВ AD , как смежные стороны квадрата;AВ AK , так как

AK ABD.

2) По признаку перпендикулярности плоскостей, для искомого построениядостаточночерезнекоторуюточкупрямойBD провести

408 Перпендикулярность прямых и плоскостей

прямую, перпендикулярную плоскости ABC. А для этого достаточ- но через эту точку провести прямую, параллельную прямойAK.

Действительно, по условию, прямая AK перпендикулярна плос- костиABC и потому, согласно теореме о двух параллельных пря-

Теорема 2 (о перпендикуляре к линии пересечения перпенди- кулярных плоскостей).

Если две плоскости перпендикулярны, то прямая, принадлежащая одной плоскости и перпендикулярная линии пересечения этих плоскостей, перпендикулярна второй плоскости.

 Пусть перпендикулярные плоскости

α и β пересекаются по прямой с, а прямаяb в плоскости β перпендикулярна прямойс и пересекает ее в точкеВ (рис. 425). По опре-

делению перпендикулярности плоскостей, в плоскости β через точку В проходит прямая

b 1 ,перпендикулярная плоскости α. Понятно, что она перпендикулярна прямойс . Но че-

рез точку прямой в плоскости можно провес- ти лишь одну прямую, перпендикулярную данной прямой. Поэтому

прямые b иb 1 совпадают. А это означает, что прямая одной плоскос- ти, перпендикулярная линии пересечения двух перпендикулярных плоскостей, перпендикулярна второй плоскости. ■

Применим рассмотренную теорему к обоснованию еще одного признака перпендикулярности плоскостей, важного с точки зре- ния последующего изучения взаимного расположения двух плос- костей.

Пустьплоскостиαиβперпендикулярны, прямая с - линия их пересечения. Через произвольную точкуА прямойс проведем

в плоскостях α и β прямые а иb, перпен- дикулярные прямойс (рис. 426). По теоре-

ме 2, прямые а иb перпендикулярны соот- ветственно плоскостям β и α, поэтому они перпендикулярны между собой:а b . Пря-

мые а иb определяют некоторую плоскость γ. Линия пересеченияс плоскостей α и β

перпендикулярна плоскости γ, по признаку перпендикулярности прямой и плоскости (теорема 1 § 18): с а , с b , а γ, b γ. Если учесть произвольность выбора точкиА на прямойс и тот факт, что через точкуА прямойс проходит единственная плоскость, ей перпендикулярная, то можно сделать следующий вывод.

Теорема 3 (о плоскости, перпендикулярной линии пересече- ния перпендикулярных плоскостей).

Плоскость, перпендикулярная линии пересечения двух перпендикулярных плоскостей, пересекает эти плоскости по перпендикулярным прямым.

Таким образом, установлено еще одно свойство перпендику- лярных плоскостей. Это свойство является характеристическим, то есть если оно справедливо для некоторых двух плоскостей, то плоскости перпендикулярны между собой. Имеем еще один при- знак перпендикулярности плоскостей.

Теорема 4 (второй признак перпендикулярности плоскос- тей).

Если прямые пересечения двух плоскостей третьей плоскостью, перпендикулярной линии их пересечения, перпендикулярны, то данные плоскости тоже перпендикулярны.

 Пусть плоскости α и β пересекаются по прямойс , и плоскость γ, перпендикулярная прямойс , пересекает плоскости α и β соот-

ветственно по прямым а иb (рис. 427). По условию,а b . Поскольку γс , тоа с. А поэтому прямаяа перпендикулярна плос- кости β, по признаку перпендикулярности прямой и плоскости (теорема 1 § 18). Отсю-

да вытекает, что плоскости α и β перпенди- кулярны, по признаку перпендикулярнос- ти плоскостей (теорема 1).■

Заслуживают внимания и теоремы о связях перпендикуляр- ности двух плоскостей третьей плоскости с их взаимным распо- ложением.

Теорема 5 (о линии пересечения двух плоскостей, перпендику- лярных третьей плоскости).

Если две плоскости, перпендикулярные третьей плоскости, пересекаются, то линия их пересечения перпендикулярна этой плоскости.

 Пусть плоскости α и β, перпендикулярные плоскости γ, пере- секаются по прямойа (a || γ), иА - точка пересечения прямойа с

Рассмотрим теорему, описывающую связь между параллель- ностью и перпендикулярностью плоскостей. Соответствующий ре- зультат мы уже имели для прямых и плоскостей.

Теорема 6 (о параллельных плоскостях, перпендикулярных третьей плоскости).

Если одна из двух параллельных плоскостей перпендикулярна третьей, то и вторая плоскость перпендикулярна ей.

 Пусть плоскости α и β парал- лельны, а плоскость γ перпендикуляр- на плоскости α. Поскольку плоскость γ

пересекает плоскость α, то она должна пересекать и параллельную ей плос- кость β. Возьмем в плоскости α про-

извольную прямую m , перпендику- лярную плоскости γ, и проведем через нее, а также через произвольную точ- ку плоскости β, плоскость δ (рис. 429).

Плоскости δ и β пересекаются по прямой п, а поскольку α║ β, тот ║ п (теорема 2 §18). Из теоремы 1 вытекает, чтоп γ, а потому перпендикулярной плоскости γ будет и плоскость β, проходящая через прямуюп. ■

Доказанная теорема дает еще один признак перпендикуляр- ности плоскостей.

Через заданную точку провести плоскость, перпендикулярную данной, можно с помощью признака перпендикулярности плоскос- тей (теорема 1). Достаточно через эту точку провести прямую, пер- пендикулярную данной плоскости (см. задачу 1 § 19). А затем через построеннуюпрямуюпровестиплоскость.Онабудетперпендикуляр- ной данной плоскости по указанному признаку. Понятно, что таких плоскостей можно провести бесконечное множество.

Более содержательной является задача о построении плоскос- ти, перпендикулярной данной, при условии, что она проходит че- рез данную прямую. Понятно, что если данная прямая перпенди- кулярна данной плоскости, то таких плоскостей можно построить бесконечное множество. Осталось рассмотреть случай, когда дан- ная прямая не перпендикулярна данной плоскости. Возможность такого построения обоснована на уровне физических моделей прямых и плоскостей в примере 1.

З а д а ч а 1 . Доказать, что через произвольную прямую, не пер- пендикулярную плоскости, можно провести плоскость, перпенди- кулярную данной плоскости.

 Пусть даны плоскость α и прямаяl , l B\ a. Возьмём на прямойl произвольную точкуМ и проведем через нее прямуют, перпен- дикулярную плоскости α (рис. 430, а). Поскольку, по условию,l не перпендикулярна α, то прямыеl ит пересекаются. Через эти прямые можно провести плоскость β (рис. 430, б), которая, соглас- но признаку перпендикулярности плоскостей (теорема 1), будет перпендикулярной плоскости α. ■

П р и м е р 3 . Через вершинуА правильной пирамидыSABC с основаниемABC провести прямую, перпендикулярную плоскости боковой граниSBC.

 Для решения данной задачи воспользуемся теоремой о пер- пендикуляре к линии пересечения перпендикулярных плоскостей

(теорема 2). Пусть K - середина ребраBC (рис. 431). ПлоскостиAKS иBCS перпенди- кулярны, по признаку перпендикулярнос- ти плоскостей (теорема 1). Действительно,ВС SK иВС АK , как медианы, проведен- ные к основаниям в равнобедренных тре­ угольниках. Поэтому, по признаку перпенди- кулярности прямой и плоскости (теорема 1 §18), прямаяВС перпендикулярна плоскостиAKS. ПлоскостьBCS проходит через прямую, перпендикулярную плоскостиAKS.

Построение. Проведем в плоскостиAKS из точкиA прямуюAL , перпендикулярную прямойKS - линии пересечения плоскостейAKS иBCS (рис. 432). По теореме о перпен- дикуляре к линии пересечения перпендику- лярных плоскостей (теорема 2), прямаяAL перпендикулярна плоскостиBCS. ■

2. На рис. 434 изображена правиль - ная четырехугольная пирамида

SABCD, точки P, M, N -середи -

ны рёбер AB, BC, BS, O -центр основания ABCD.Какие из пар плос - костей перпендикулярны:

1) ACS и BDS;2) MOSи POS;

3) COS и MNP; 4) MNPи SOB;

5) CND и ABS?

3) PACи PBC; 4) PACи PAB?

4. Две плоскости перпендикулярны. Можно ли через произвольную точку одной из них провести прямую в этой плоскости, второй плоскости?

5. В плоскости α нельзя провести прямую, плоскости β. Могут ли эти плоскости быть ми?

6. Через некоторую точку плоскости α проходит щая в этой плоскости и перпендикулярная плоскости ли, что плоскости α и β перпендикулярны?

Секция забора прикреплена к вертикальному столбу ли утверждать, что плоскость забора вертикальна?

Как к рейке, параллельной поверхности земли, прикрепить вертикально щит?

Почему поверхность дверей, независимо от того, закрыты они или открыты, располагается вертикально к полу?

Почему отвес плотно прилегает к вертикальной стене, а к на- клонной - не обязательно?

Можно ли к наклонному столбу прикрепить щит так, чтобы он был перпендикулярен поверхности земли?

Как на практике установить, перпендикулярна ли плоскость

стены плоскости пола? перпендикулярнуюперпендикулярнуюперпендикулярны - прямая, лежа - β. Верно 7. . Можно 8.9.10.11.12.

Графические упражнения

1. На рис. 436 изображен куб ABCDA 1 B 1 C 1 D 1 .

1) Укажите плоскости, перпендикулярные плоскости ВDD 1 .

2) Как расположены плоскости и

A1 B1 CAB 1 C 1

421. ОтрезокOS проведен из центраО квадратаABCD перпен- дикулярно его плоскости.

1°) Определите взаимное расположение плоскостей ACS

и АВС.

2°) Определите взаимное расположение плоскостей ACS

и BDS .

3) Постройте плоскость, проходящую через прямую OS пер- пендикулярно плоскостиABS.

4) Постройте плоскость, перпендикулярную плоскости АВС и проходящую через середины сторонAD иCD.

422. Из точки пересеченияO диагоналей ромбаABCD проведен перпендикулярный плоскости ромба отрезокOS ;AB = DB =

1°) Определите взаимное расположение плоскостей SDB и

ABC, SDBи ACS.

2°) Постройте плоскость, проходящую через прямую BC пер- пендикулярно плоскостиABD.

3) Проведите через середину F отрезкаCS плоскость, пер- пендикулярную плоскостиАВС.

4) Найдите площадь треугольника BDF.

423. Дан куб ABCDA1 B1 C1 D1 .

1°) Определите взаимное расположение плоскостей АВ 1 С 1

и CDD1 .

2°) Определите взаимное расположение плоскостей АВ 1 С 1

и CD1 A1 .

3°) Постройте плоскость, проходящую через точку А перпен- дикулярно плоскостиBB 1 D 1 .

4) Постройте сечение куба плоскостью, проходящей через се- редины рёберА 1 D 1 иB 1 C 1 перпендикулярно плоскостиАВС. 5)ОпределитевзаимноерасположениеплоскостиАА 1 В иплос- кости, проходящей через середины рёберА 1 В 1 , C 1 D 1 , CD.

6) Найдите площадь сечения куба плоскостью, проходящей через ребро ВВ 1 и середину ребраA 1 D 1 (ВВ 1 = а ).

7) Постройте точку, симметричную точке А относительно плоскостиA 1 B 1 C.

424. В правильном тетраэдреАBCD с ребром 2 см точкаМ - се- рединаDВ , а точкаN - серединаАС.

1°) Докажите, что прямая DВ перпендикулярна плоскости

2°) Докажите, что плоскость ВDМ перпендикулярна плос- костиАМС.

3) Через точку О пересечения медиан треугольникаАDС проведите прямую, перпендикулярную плоскостиАМС.

4) Найдите длину отрезка этой прямой внутри тетраэдра. 5) В каком отношении плоскость АМС делит этот отрезок?

425. Два равносторонних треугольникаАВС иADC лежат в пер- пендикулярных плоскостях.

1°) Найдите длину отрезка BD, еслиAC = 1 см.

2) Докажите, что плоскость BKD (K лежит на прямойAC ) перпендикулярна плоскости каждого из треугольников тог- да и только тогда, когдаK является серединой стороныAC.

426. ПрямоугольникABCD, стороны которого 3 см и 4 см, пере- гнули по диагоналиAC так, что треугольникиABC иADC расположились в перпендикулярных плоскостях. Опреде- лите расстояние между точкамиB иD после того, как пере- гнули прямоугольникABCD.

427. Через данную точку проведите плоскость, перпендикуляр- ную каждой из двух данных плоскостей.

428°. Докажите, что плоскости смежных граней куба перпендику- лярны.

429. Плоскости α и β перпендикулярны между собой. Из точкиА плоскости α проведена перпендикулярная плоскости β пря- маяАВ. Докажите, что прямаяАВ лежит в плоскости α.

430. Докажите, что если плоскость и прямая, не лежащая в этой плоскости, перпендикулярны одной и той же плоскости, то они параллельны между собой.

431. Через точкиА иВ , лежащие на линии пересеченияр пер- пендикулярных между собой плоскостей α и β, проведены перпендикулярныер прямые:АА 1 в α, ВВ 1 в β. ТочкаX ле- жит на прямойАА 1 , а точкаY - наВB 1 . Докажите, что пря- маяВB 1 перпендикулярна прямойВХ , а прямаяАA 1 пер- пендикулярна прямойАY.

432*. Через середину каждой стороны треугольника проведена плоскость, перпендикулярная этой стороне. Докажите, что все три проведенные плоскости пересекаются по одной пря- мой, перпендикулярной плоскости треугольника.

Упражнения для повторения

433. В равностороннем треугольнике со стороной b определите: 1) высоту; 2) радиусы вписанной и описанной окружностей.

434. Из одной точки проведен к данной прямой перпендикуляр и две наклонные. Определите длину перпендикуляра, если наклонные равны 41 см и 50 см, а их проекции на данную прямую относятся, как 3: 10.

435. Определите катеты прямоугольного треугольника, если бис - сектриса прямого угла делит гипотенузу на отрезки 15 см и

Основное определение

Две плоскости называ-

ются перпендикуляр­ ными, если каждая из них образована прямы - ми, перпендикулярны - ми второй плоскости и проходящими через точки пересечения этих плоскостей.

Данная статья посвящена перпендикулярным плоскостям. Будут даны определения, обозначения вместе с примерами. Будет сформулирован признак перпендикулярности плоскостей и условие, при котором он выполним. Будут рассмотрены решения подобных задач на примерах.

Yandex.RTB R-A-339285-1

При наличии угла между пересекающимися прямыми можно говорить об определении перпендикулярных плоскостей.

Определение 1

При условии, что угол между перпендикулярными прямыми равен 90 градусов, их называют перпендикулярными.

Обозначение перпендикулярности принято писать знаком « ⊥ ». Если в условии дано, что плоскости α и β перпендикулярные, тогда запись принимает вид α ⊥ β . На рисунке ниже показано подробно.

Когда в улови дано, что плоскость α и β перпендикулярны, это значит, что α перпендикулярна β и наоборот. Такие плоскости называют взаимно перпендикулярными. Например, стена и потолок в комнате являются взаимно перпендикулярными, так как при пересечении дают прямой угол.

Перпендикулярность плоскостей – признак и условие перпендикулярности

На практике можно встретить задания, где необходимо определить перпендикулярность заданных плоскостей. Для начала нужно определить угол между ними. Если он равен 90 градусам, тогда они считаются перпендикулярными из определения.

Для доказательства перпендикулярности двух плоскостей применяют признак перпендикулярности двух плоскостей.Формулировка содержит понятия перпендикулярная прямая и плоскость. Напишем точное определение признака перпендикулярности в виде теоремы.

Теорема 1

Если одна из двух заданных плоскостей пересекает прямую, перпендикулярную другой плоскости, то заданные плоскости перпендикулярны.

Доказательство имеется в учебнике по геометрии за 10 - 11 класс, где есть подробное описание. Из признака следует, что, если плоскость перпендикулярна линии пересечения двух заданных плоскостей, то она перпендикулярна к каждой из этих плоскостей.

Существует необходимое и достаточное условия для доказательства. Рассмотрим их для перпендикулярности двух заданных плоскостей, которое применяется в качестве проверки их перпендикулярности, находящихся в прямоугольной системе координат трехмерного пространства. Чтобы доказательство имело силу, необходимо применить определение нормального вектора плоскости, который способствует доказать необходимое и достаточное условие перпендикулярности плоскостей.

Теорема 2

Для того, чтобы перпендикулярность пересекающихся плоскостей была явной, необходимо и достаточно, чтобы нормальные векторы заданных плоскостей пересекались под прямым углом.

Доказательство

Пусть в трехмерном пространстве задана прямоугольная система координат. Если имеем n 1 → = (A 1 , B 1 , C 1) и n 2 → = (A 2 , B 2 , C 2) , являющимися нормальными векторами заданных плоскостей α и β , то необходимым и достаточным условием перпендикулярности векторов n 1 → и n 2 → примет вид

n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0

Отсюда получаем, что n 1 → = (A 1 , B 1 , C 1) и n 2 → = (A 2 , B 2 , C 2) - нормальные векторы заданных плоскостей, а для действительности перпендикулярности α и β необходимо и достаточно, чтобы скалярное произведение векторов n 1 → и n 2 → было равным нулю, а значит, принимало вид n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + C 1 · C 2 = 0 .

Равенство выполнено.

Рассмотрим подробнее на примерах.

Пример 1

Определить перпендикулярность плоскостей, заданных в прямоугольной системе координат O x y z трехмерно пространства, заданного уравнениями x - 3 y - 4 = 0 и x 2 3 + y - 2 + z 4 5 = 1 ?

Решение

Для нахождения ответа на вопрос о перпендикулярности для начал необходимо найти координаты нормальных векторов заданных плоскостей, после чего можно будет выполнить проверку на перпендикулярность.

x - 3 y - 4 = 0 является общим уравнением плоскости, из которого можно сразу преобразовать координаты нормального вектора, равные n 1 → = (1 , - 3 , 0) .

Для определения координаты нормального вектора плоскости x 2 3 + y - 2 + z 4 5 = 1 перейдем от уравнения плоскости в отрезках к общему.

Тогда получим:

x 2 3 + y - 2 + z 4 5 ⇔ 3 2 x - 1 2 y + 5 4 z - 1 = 0

Тогда n 2 → = 3 2 , - 1 2 , 5 4 - это координаты нормального вектора плоскости x 2 3 + y - 2 + z 4 5 = 1 .

Перейдем к вычислению скалярного произведения векторов n 1 → = (1 , - 3 , 0) и n 2 → = 3 2 , - 1 2 , 5 4 .

Получим, что n 1 → , n 2 → = 1 · 3 2 + (- 3) · - 1 2 + 0 · 5 4 = 3 .

Видим, что оно не равно нулю, значит, что заданные векторы не перпендикулярны. Отсюда следует, что плоскости также не перпендикулярны. Условие не выполнено.

Ответ: плоскости не перпендикулярны.

Пример 2

Прямоугольная система координат O x y z имеет четыре точки с координатами A - 15 4 , - 7 8 , 1 , B 17 8 , 5 16 , 0 , C 0 , 0 , 3 7 , D - 1 , 0 , 0 . Проверить, перпендикулярны ли плоскости А В С и A B D .

Решение

Для начала необходимо рассчитать скалярное произведение векторов данных плоскостей. Если оно равно нулю, только в этом случае можно считать, что они перпендикулярны. Находим координаты нормальных векторов n 1 → и n 2 → плоскостей А В С и A B D .

Из заданных координат точек вычислим координаты векторов A B → , A C → , A D → . Получаем, что:

A B → = 47 8 , 19 16 , - 1 , A C → = 15 4 , 7 8 , - 4 7 , A D → = 11 4 , 7 8 , - 1 .

Нормальный вектор плоскости А В С является векторным произведением векторов A B → и A C → , а для A B D векторное произведение A B → и A D → . Отсюда получим, что

n 1 → = A B → × A C → = i → j → k → 47 8 19 16 - 1 15 4 7 8 - 4 7 = 11 56 · i → - 11 28 · j → + 11 16 · k → ⇔ n 1 → = 11 56 , - 11 28 , 11 16 n 2 → = A B → × A D → = i → j → k → 47 8 19 16 - 1 11 4 7 8 - 1 = - 5 16 · i → + 25 8 · j → + 15 8 · k → ⇔ n 2 → = - 5 16 , 25 8 , 15 8

Приступим к нахождению скалярного произведения n 1 → = 11 56 , - 11 28 , 11 16 и n 2 → = - 5 16 , 25 8 , 15 8 .

Получим: n 1 → , n 2 → = 11 56 · - 5 16 + - 11 28 · 25 8 + 11 16 · 15 8 = 0 .

Если оно равно нулю, значит векторы плоскостей А В С и A B D перпендикулярны, тогда и сами плоскости перпендикулярны.

Ответ: плоскости перпендикулярны.

Можно было подойти к решению иначе и задействовать уравнения плоскостей А В С и A B D . После нахождения координат нормальных векторов данных плоскостей можно было бы проверить на выполнимость условие перпендикулярности нормальных векторов плоскостей.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Понятие перпендикулярных плоскостей

При пересечении двух плоскостей у нас получается $4$ двугранных угла. Два угла равны $\varphi $, а два другие равны ${180}^0-\varphi $.

Определение 1

Углом между плоскостями называется минимальный из двугранных углов, образованных этими плоскостями.

Определение 2

Две пересекающиеся плоскости называются перпендикулярными, если угол между этими плоскостями равен $90^\circ$ (рис. 1).

Рисунок 1. Перпендикулярные плоскости

Признак перпендикулярности двух плоскостей

Теорема 1

Если прямая плоскости перпендикулярна другой плоскости, то эти плоскости перпендикулярны друг другу.

Доказательство.

Пусть нам даны плоскости $\alpha $ и $\beta $, которые пересекаются по прямой $AC$. Пусть прямая $AB$, лежащая в плоскости $\alpha $ перпендикулярна плоскости $\beta $ (рис. 2).

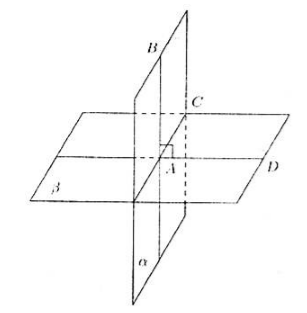
Рисунок 2.

Так как прямая $AB$ перпендикулярна плоскости $\beta $, то она перпендикулярна и прямой $AC$. Проведем дополнительно прямую $AD$ в плоскости $\beta $, перпендикулярно прямой $AC$.

Получаем, что угол $BAD$ - линейный угол двугранного угла, равный $90^\circ$. То есть, по определению 1, угол между плоскостями равен $90^\circ$, значит, данные плоскости перпендикулярны.

Теорема доказана.

Из этой теоремы следует следующая теорема.

Теорема 2

Если плоскость перпендикулярна прямой, по которой пересекаются две другие плоскости, то она перпендикулярна и этим плоскостям.

Доказательство.

Пусть нам даны две плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Плоскость $\gamma $ перпендикулярна прямой $c$ (рис. 3)

Рисунок 3.

Так как прямая $c$ принадлежит плоскости $\alpha $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\alpha $ и $\gamma $ перпендикулярны.

Так как прямая $c$ принадлежит плоскости $\beta $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\beta $ и $\gamma $ перпендикулярны.

Теорема доказана.

Для каждой из этих теорем справедливы и обратные утверждения.

Примеры задач

Пример 1

Пусть нам дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Найти все пары перпендикулярных плоскостей (рис. 5).

Рисунок 4.

Решение.

По определению прямоугольного параллелепипеда и перпендикулярных плоскостей видим следующие восемь пар перпендикулярных между собой плоскостей: $(ABB_1)$ и $(ADD_1)$, $(ABB_1)$ и $(A_1B_1C_1)$, $(ABB_1)$ и $(BCC_1)$, $(ABB_1)$ и $(ABC)$, $(DCC_1)$ и $(ADD_1)$, $(DCC_1)$ и $(A_1B_1C_1)$, $(DCC_1)$ и $(BCC_1)$, $(DCC_1)$ и $(ABC)$.

Пример 2

Пусть нам даны две взаимно перпендикулярные плоскости. Из точки одной плоскости проведен перпендикуляр к другой плоскости. Доказать, что эта прямая лежит в данной плоскости.

Доказательство.

Пусть нам даны перпендикулярные плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Из точки $A$ плоскости $\beta $ проведен перпендикуляр $AC$ к плоскости $\alpha $. Предположим, что $AC$ не лежит в плоскости $\beta $ (рис. 6).

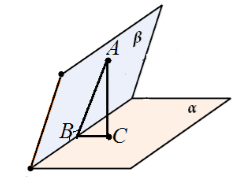
Рисунок 5.

Рассмотрим треугольник $ABC$. Он является прямоугольным с прямым углом $ACB$. Следовательно, $\angle ABC\ne {90}^0$.

Но, с другой стороны, $\angle ABC$ является линейным углом двугранного угла, образованного этими плоскостями. То есть двугранный угол, образованный этими плоскостями не равняется 90 градусам. Получаем, что угол между плоскостями не равен $90^\circ$. Противоречие. Следовательно, $AC$ лежит в плоскости $\beta $.